Learning Temporal Dynamics from Cycles in Narrated Video

Dave Epstein
UC Berkeley Jiajun Wu
Stanford University Cordelia Schmid
Google Chen Sun
Google, Brown University
Paper
Teaser figure
Predicting the future is challenging. Given a frame a at time t, previous work focuses on predicting frames at a fixed offset, such as b. These frames are often redundant or stochastic, motivating the prediction of non-immediate futures. Predicting such a frame is difficult, as many futures are irrelevant, such as b. Aided by narrations in video, we can learn long-term temporal dynamics in video, and predict d. We learn these dynamics with a multi-modal temporal cycle consistency problem.

Learning to model how the world changes as time elapses has proven a challenging problem for the computer vision community. We propose a self-supervised solution to this problem using temporal cycle consistency jointly in vision and language, training on narrated video. Our model learns modality-agnostic functions to predict forward and backward in time, which must undo each other when composed. This constraint leads to the discovery of high-level transitions between moments in time, since such transitions are easily inverted and shared across modalities.

We justify the design of our model with an ablation study on different configurations of the cycle consistency problem. We then show qualitatively and quantitatively that our approach yields a meaningful, high-level model of the future and past. We apply the learned dynamics model without further training to various tasks, such as predicting future action and temporally ordering sets of images.

Paper

@InProceedings{Epstein_2021_ICCV,
  title={Learning Temporal Dynamics from Cycles in Narrated Video},
  author={Epstein, Dave and Wu, Jiajun and Schmid, Cordelia and Sun, Chen.},
  booktitle = {Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV)},
  month = {October},
  year = {2021}
}

Learning to cycle through time

Given an image (here, second from left) as a start node, our model finds corresponding text to build a start state. From this, our model predicts a future image and again builds a multi-modal state. Finally, our model predicts a past image from the future state. The discrepancy between this prediction of the past and the start image gives our cycle-consistency loss. To solve this problem, we learn the temporal and cross-modal edges using soft attention.

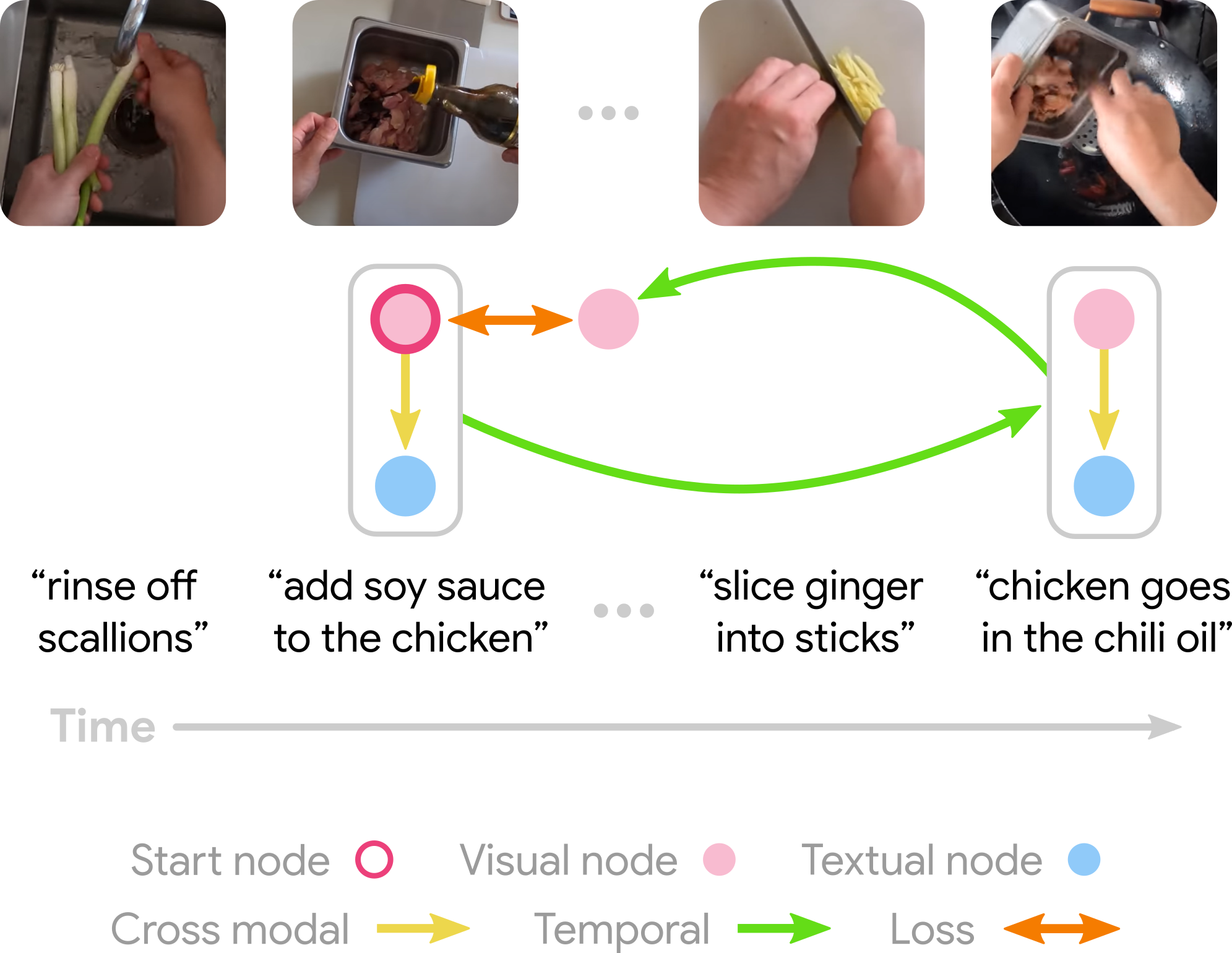
Discovered temporal dynamics

After being trained, our model learns to cycle through video, using both visual and textual information. We show some examples of cycles identified by our model, which capture complex transitions between states.

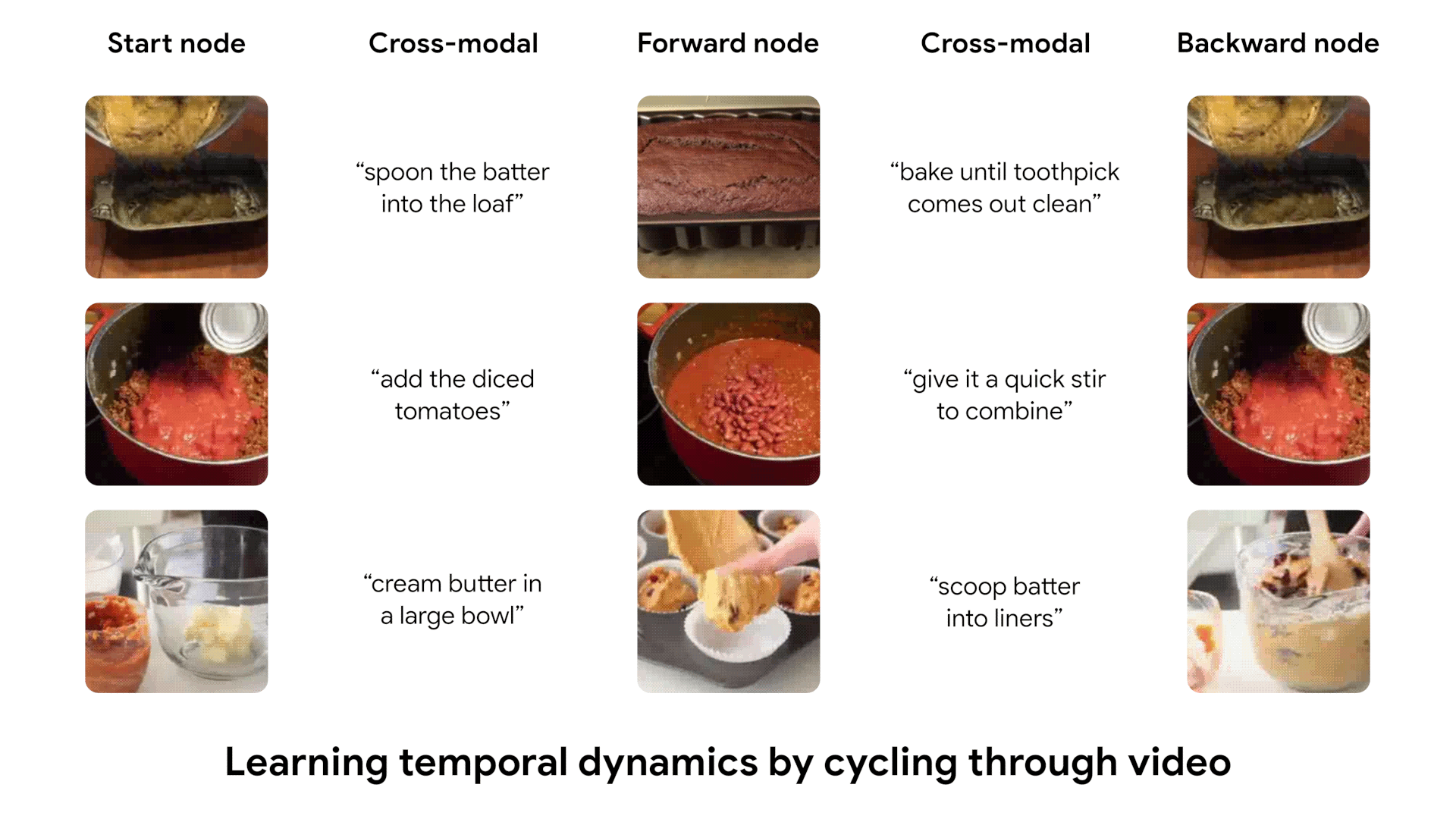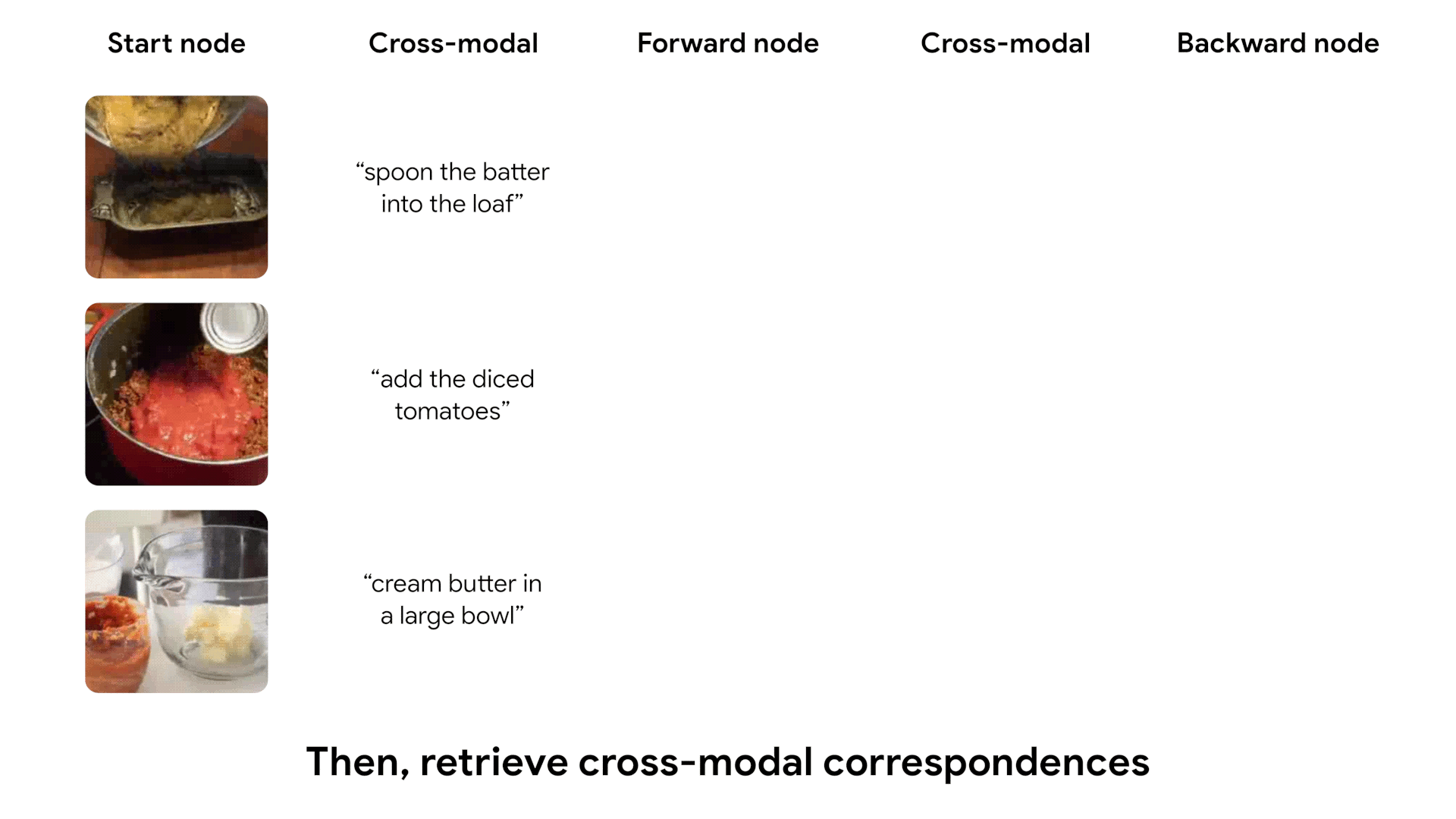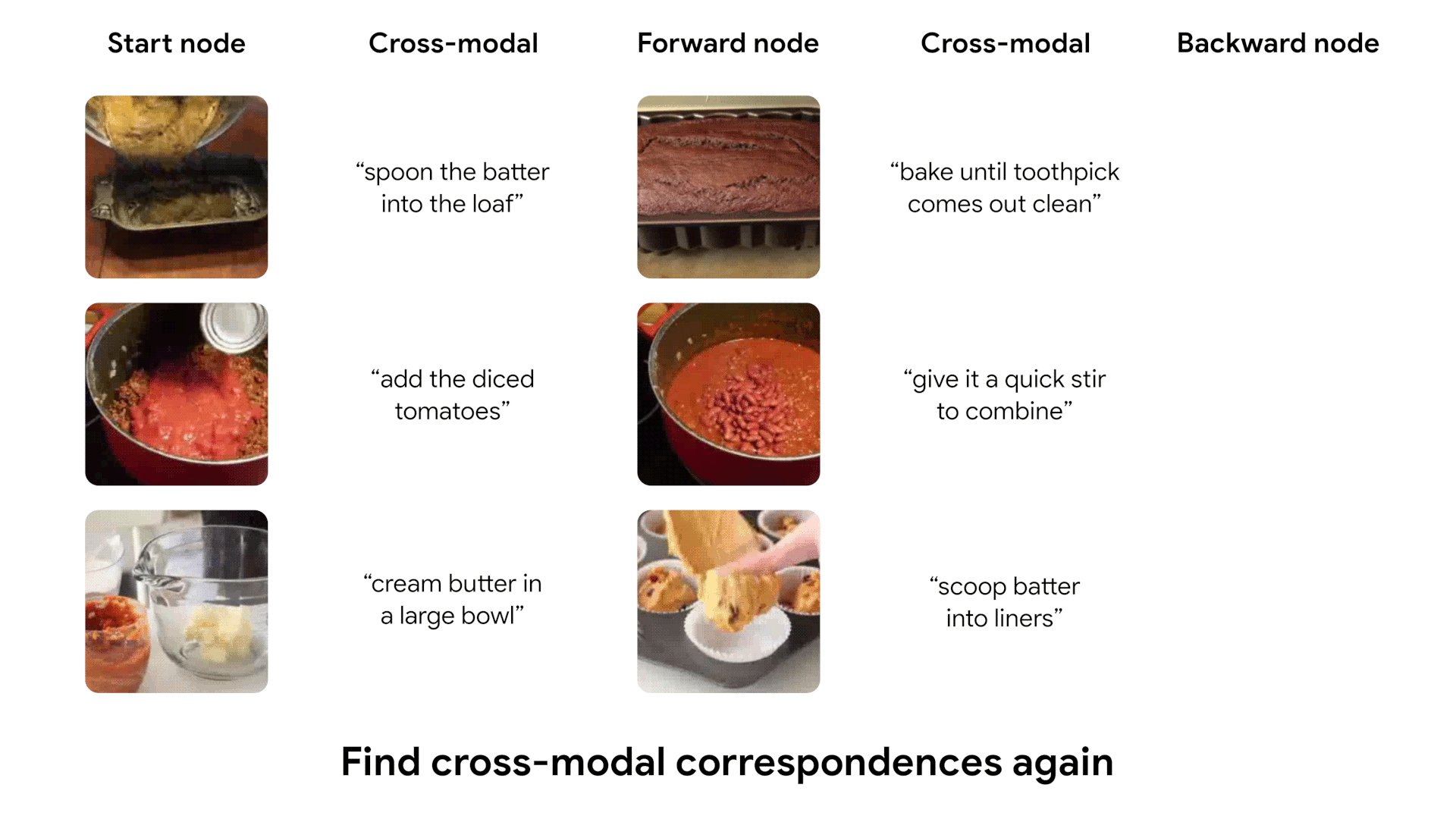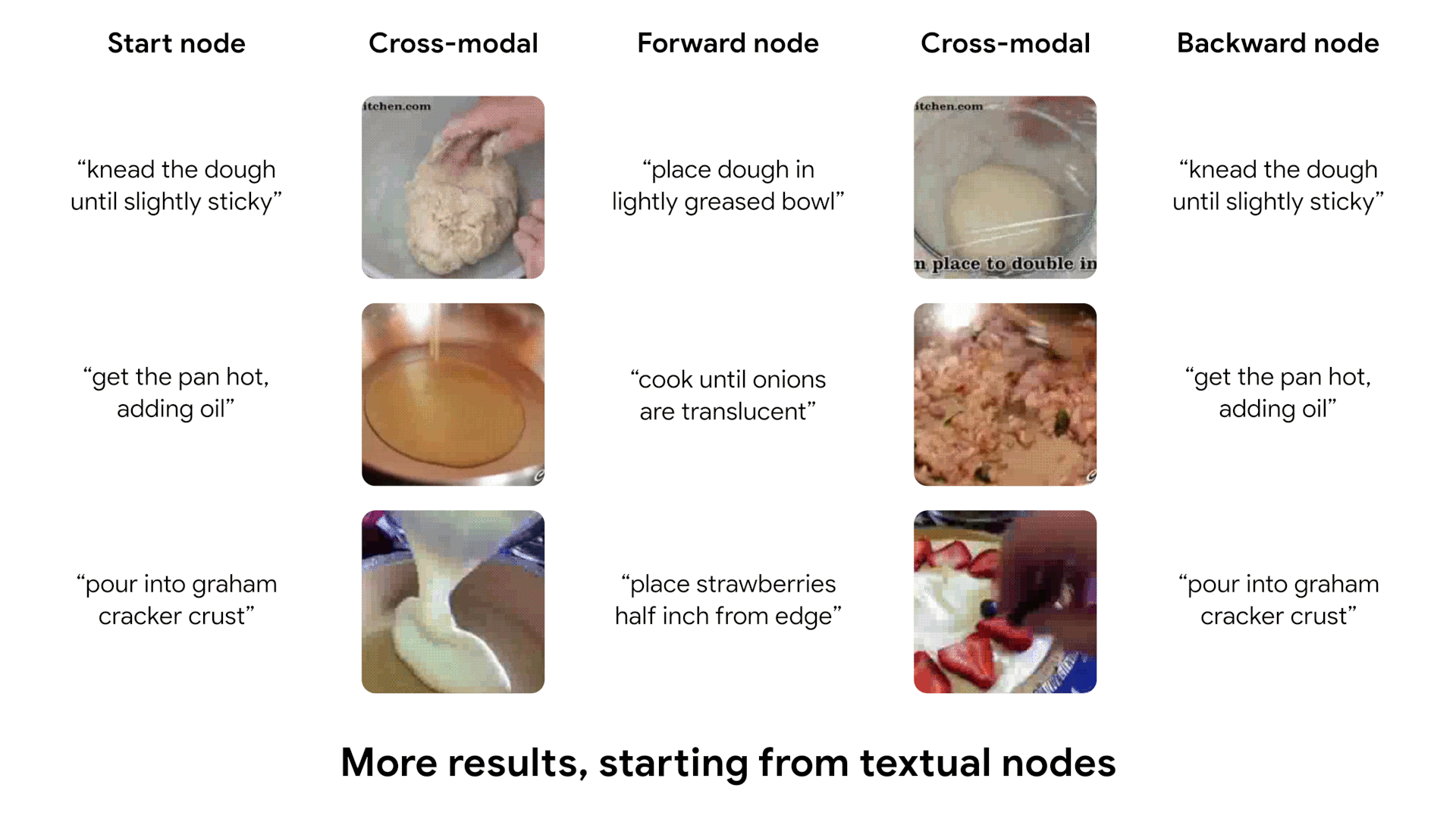
Most salient transitions in videos

We can run our learned model on entire videos to identify the most salient temporal transitions. We define a likelihood score for each pair of frames in a video, according to our model's predictions. We then show the highest-score pair of frames in each video.

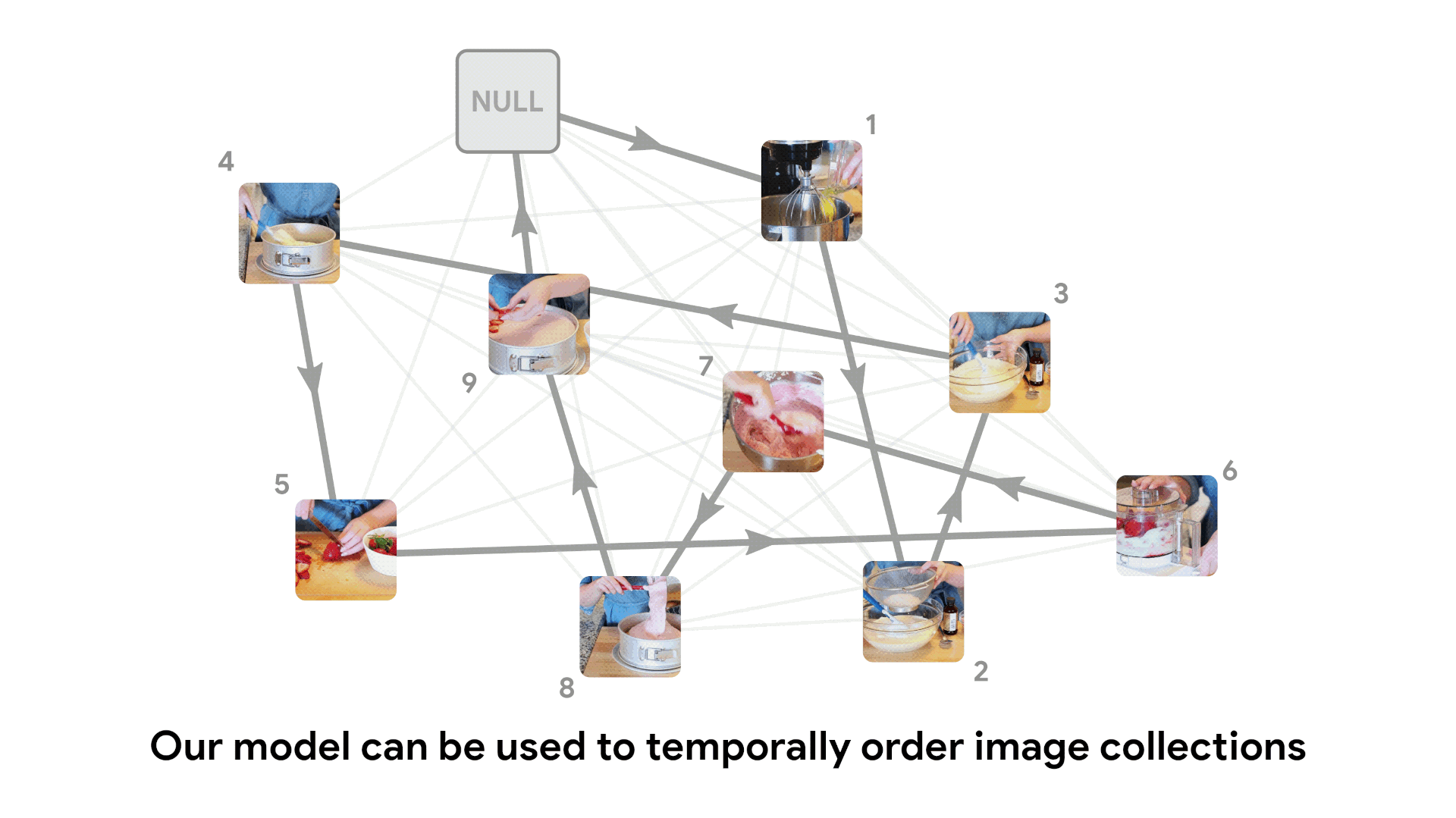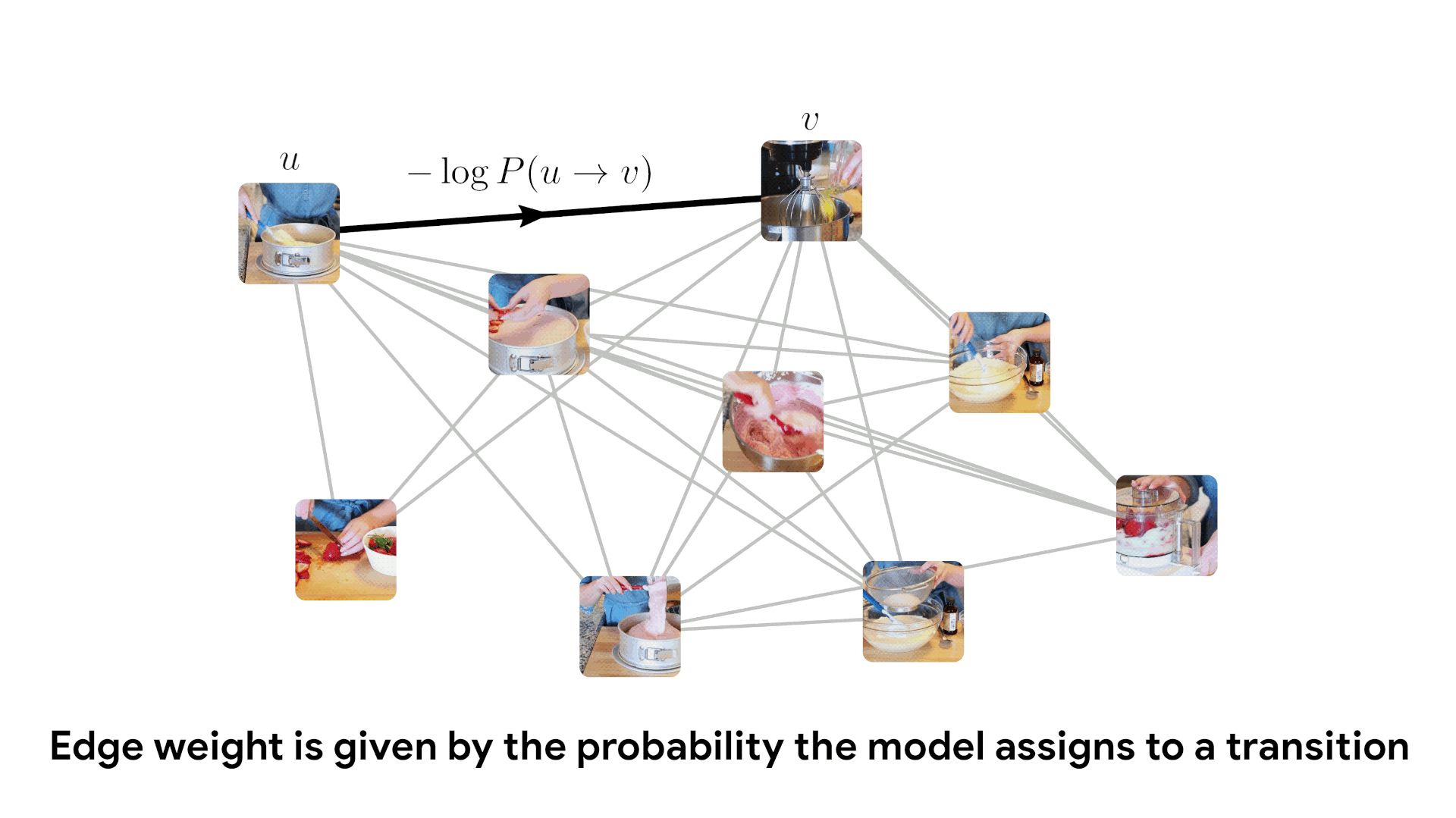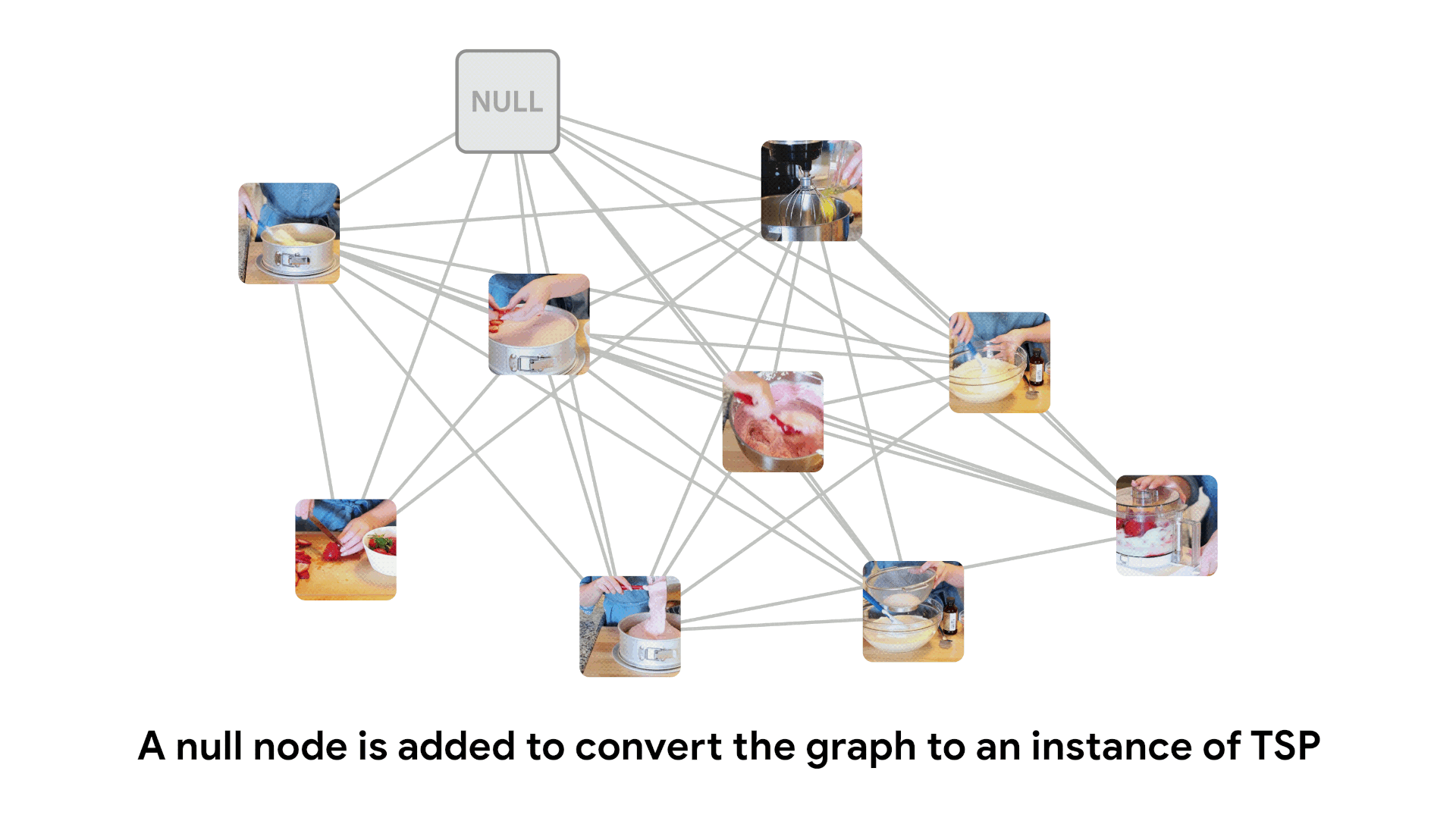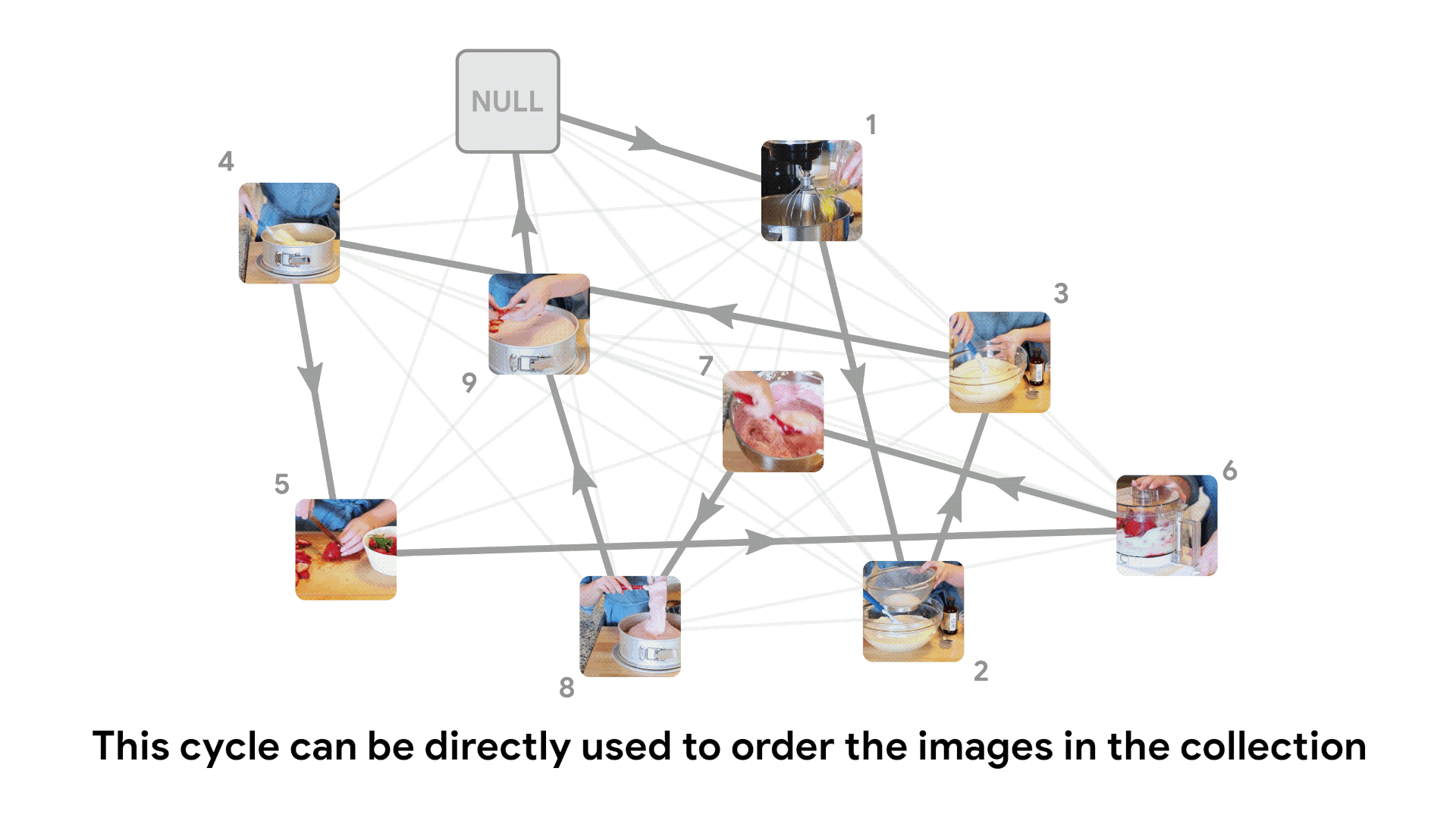
Unshuffling image collections

We can use this same likelihood score to temporally sort an unordered collection of video frames, by finding a globally optimal explanation for the data.

We do this by creating a fully connected bidirectional graph where edge weight is given by the negative log score. This graph can be viewed as an instance of the traveling salesman problem, and solved using classical algorithms. The optimal TSP path gives the most likely ordering of frames.

Acknowledgements

This work was done while Dave Epstein was a student researcher at Google. We thank Alexei Efros, Mia Chiquier, and Shiry Ginosar for their feedback, and Allan Jabri for inspiration in figure design. Dave would like to thank Dídac Surís and Carl Vondrick for insightful early discussions on cycling through time in video.